Qstats is a good place to start in analyzing your data. It computes
some basic statistics on the quantitative traits and summarizes missing
data.
Let
![]() be a vector of quantitative trait values. For each trait in turn, it calculates the
sample size (n),
mean (
be a vector of quantitative trait values. For each trait in turn, it calculates the
sample size (n),
mean (
![]() ),
variance (
),
variance (
![]() ),
standard deviation (
),
standard deviation (
![]() ),
skewness,
kurtosis and average deviation,
),
skewness,
kurtosis and average deviation,
![]() . The coefficient of variation is the
sample standard deviation divided by the sample mean.
. The coefficient of variation is the
sample standard deviation divided by the sample mean.
lynchwalsh@98 provide a lucid explanation of some of the
statistics calculated by Qstats.
Let the ![]() th sample moment be
th sample moment be
![]() . Clearly,
. Clearly,
![]() . Using the notation
. Using the notation
![]() , we can estimate the
sample variance with
, we can estimate the
sample variance with
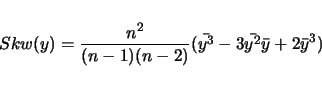
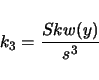
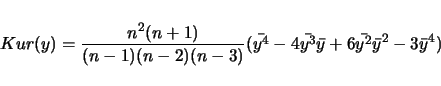
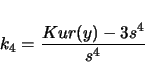
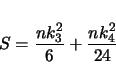
An example of the output follows:
------------------------------------------------------ ------------------------------------------------------ This is for -trait 1 called szfreq ------------------------------------------------------ Sample Size................ 119 M(1)....................... 0.4349 M(2)....................... 0.2184 M(3)....................... 0.1195 M(4)....................... 0.0694 Mean Trait Value........... 0.4349 Variance................... 0.0295 Standard Deviation......... 0.1718 Coefficient of Variation... 0.3951 Average Deviation.......... 0.1398 Skw..LW(24)................ -0.0010 .....Sqrt(6/n)............. 0.2245 Kur..LW(29)................ 0.0022 .....Sqrt(24/n)............ 0.4491 k3...LW(24)................ -0.1922 k4...LW(28)................ -0.5250 S (5%: 5.99, 1%: 9.21)..... 2.0992 ------------------------------------------------------ ------------------------------------------------------In the above example, LW(i) refers to a page number in lynchwalsh@98 where one can find an explanation of the quantity. The value of the test statistic
After the basic statistics, Qstats draws a histogram of the quantitative trait. It is a simple histogram in that the range of the data are divided into 50 equally sized bins, and the number of data points falling into each bin are counted and plotted. A small table following the histogram gives the sample size, minimum, first quartile, median, second quartile and maximum.